مفهوم اللانهاية وفندق هيلبرت

 مفهوم المالانهاية - الأغرب في الرياضيات

مفهوم المالانهاية أو اللانهاية هو مفهوم معقد ويمكن أن نتناوله من عدة زوايا مختلفة و وجهات نظر متباينة، إذ يمكن أن تكون وجهة نظر رياضية أو فيزيائية أو فلسفية...

في هذه المقالة، لن نتطرق للحديث عنهم جميعًا بل سنركز على جانب واحد على وجه الخصوص ،ألا وهو اللانهاية في الرياضيات ، وبشكل أكثر تحديدًا المجموعات اللانهائية.

1. ماهي اللانهاية

1.1 الكاردينال في المجموعات

في الرياضيات، كثيرا ما نسمع عن المجموعات، أي مجموعة من الأشياء التي تسمى العناصر. يمكن أن تكون هذه العناصر أي شيء يخطر على بالك، كالارقام، والأشكال الهندسية، والعلامات الرياضية، والدوال ... وما يميز هذه المجموعات هو حجمها، وهو عدد العناصر التي تحتوي عليها، والذي يسمى الأصل أو الكاردينال (cardinal).

1.2 اللانهاية 

عند بداية تعلم الرياضيات، أول مجموعة أعداد نتعلمها هي مجموعة الأعداد الصحيحة الطبيعية الموجبة وهي 0 ، 1 ، 2 ، 3 ، 4 ، 5 ، إلخ ... ونسمي هذه المجموعة N  لكن ما هو الأصل أو الكاردينال لمجموعة الأعداد الطبيعية؟ كم عدد الأعداد الصحيحة الطبيعية في المجموعة  N؟

الكل يعلم أن هناك عدد لانهائي من الأعداد الصحيحة الطبيعية . ويمكننا حتى استخدام هذه الحقيقة كتعريف للما لا نهاية حيث أن اللانهاية هي كاردينال مجموعة الأعداد الطبيعية. يرمز له بهذا الرمز ∞.

من البديهي اننا  إذا أخذنا جزءًا فقط من أي مجموعة معينة، فلا بد أن يكون كاردينال هذا الجزء، أصغر من كاردينال المجموعة الأصلية ، فإذا كونت مجموعة من 5 تفاحات داخل المجموعة الأصلية (لنقل انها 10 تفاحات) ، فإن كاردينال المجموعة الأصلية (وهو 10) لا بد أن يكون اكبر من كاردينال المجموعة الفرعية (وهو 5) وهو ما يبدو منطقيًا للغاية، لكن هل نفس الشيء بنطبق على المجموعات اللانهائية؟

دعونا نرى ما يحدث للأعداد الطبيعية. لذلك سوف نأخذ في الاعتبارالأعداد الطبيعية N، ولنصنع مجموعة تحتوي على كل الاعداد الصحيحة الطبيعية إضافة الى عنصر جديد وهو -1 بحيث تبدا من  -1 ، 0 ، 1 ، 2 ، 3 ، إلخ ..  سوف نسمي هذه المجموعة الجديدة H.

السؤال هنا: ما هو أصل (أو كاردينال) هذه المجموعة الجديدة H؟
حسنًا ، الكل سيقول أنه اللانهاية وهذا صحيح فعلا، لكن في نفس الوقت الكل يعلم أن H دائمًا أكبر من N. فهل هي حقًا نفس اللانهاية أم أنها لانهاية أكبر؟ 

في الواقع لفهم هذا الامر لابد لنا من ايجاد وسيلة للتفريق بين اللانهايات.
لفهم الأمر بشكل أكبر، سنلعب لعبة فكرية تسمى فندق هيلبرت

2. فندق هيلبرت 

2.1. مفهوم التقابل

فندق هيلبرت عبارة عن لغز اقترحه عالم الرياضيات ديفيد هيلبرت لأول مرة.

لنتخيل فندقًا به عدد لا يحصى من الغرف، وهذه الغرف مرقمة بالأرقام الطبيعية ، لذا توجد غرفة رقم 0، غرفة رقم 1، غرفة رقم 2... وهكذا الى مالانهاية...

لنفترض أيضا أن جميع هذه الغرف مشغولة ويسكن كل غرفة شخص شخص واحد. كل شيء على ما يرام حتى يأتي شخص ما إلى مكتب استقبال الفندق ويسأل عما إذا كانت هناك غرفة متاحة.

الآن بما أن كل الغرف مشغولة،  سيخبره مدير الفندق انه لا توجد غرفة خالية .
لكن هذا الشخص الذي وصل للتو والذي هو في الواقع عالم رياضيات ، سيعطيه حلا يجعل الغرفة الأولى خالية، حيث سيقول له بأن ينقل كل نزيل الى الغرفة المجاورة لغرفته. حيث ينتقل الشخص الموجود حاليًا في الغرفة 0 إلى الغرفة 1 ، وينتقل الشخص الموجود في الغرفة 1 إلى الغرفة 2 ، وهكذا ... ستبقى بذلك الغرفة 0 خالية للنزيل الجديد.

بهذا نكون قد فعلنا شيئًا مثيرًا للاهتمام، أخذنا كل النزلاء في الفندق بالاضافة الى الوافد الجديد وعينا رقم غرفة جديد لهم، وبهذه الطريقة حصل كل شخص على غرفة خاصة له، بما في ذلك الوافد الجديد.

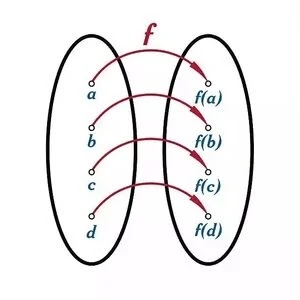
من الناحية الرياضية ، عندما نقوم بإسناد لكل عنصر من المجموعة أ عنصرا آخرا يقابله من المجموعة ب ، فإننا نطلق على هذه العملية اسم التقابل.

هناك قاعدة في الرياضيات تقول أنه إذا تمكنا من عمل تقابل بين مجموعتين فإن هتين المجموعتين لهما نفس الكاردينال أي أنهما يحتويان على نفس عدد العناصر، فالفندق يحتوي على عدد غرف مساوية لعدد النازلين فيها حتى بعد أن قمنا بإدخال نزيل اليه !!! وكذلك المجموعة H التي أنشأناها في البداية تحتوي على نفس عناصر المجموعة N وهي اللانهاية. وبذلك أصبح لدينا طريقة لمقارنة أحجام المجموعات اللانهائية ، يكفي أن نرى ما إذا كان بإمكاننا عمل تقابل بينها.

بمعنى آخر، إذا كانت لديك مجموعة ويمكنك ترقيم عناصرها، فهذا يعني أنه يمكنك إنشاء تقابل بين هذه المجموعة و N وبالتالي سيكون لهذه المجموعة نفس الكاردينال (عدد العناصر) مثل N.

عند التطرق الى اللانهائيات والتعامل معها،  يحدث شيء غريب. فالبديهي أنه عندما نأخذ مجموعة وننظر فقط في جزء فرعي من هذه المجموعة ، فإن كاردينال هذا الجزء يكزن أصغر من كاردينال المجموعة الكبيرة، لكن إذا كان كلا المجموعتين نهائيتين فإن لهما نفس عدد العناصر حتى وإن كانت المجموعة الأولى تتفرع من المجموعة الثانية. وهذه إحدى خصائص المجموعات اللانهائية.

2.2. المجموعات اللانهائية القابلة للعد

لنعد الآن الى لعبة فندق هيلبرت، تخيل أنها وصلت حافلة تحتوي على 42 شخصا يريدون جميعهم أن ينزلوا ذاك الفندق الممتلئ. ماهو الحل هنا؟ نعم كما خمنت بالضبط سننقل كل شخص 42 غرفة الى الأمام، فالشخص صاحب الغرفة 0 سينتقل إلى الغرفة 42 و صاحب الغرفة 1 الى 43 ...الخ. وسيتسع الفندق لهم جميعا بما أن الفندق يحتوي على عدد لانهائي من الغرف.

الآن ماذا يحدث إذا وصلت حافلة إلى مكتب الاستقبال وعلى متنها عدد لا نهائي من الناس. هل بإمكاننا ايجاد مكان للجميع في الفندق؟

الاجابة هي نعم، ولكن كيف؟ للقيام بذلك ، ما عليك سوى إخبار أولئك الموجودين بالفعل في الفندق بأخذ الغرفة المرقمة ضعف غرفتهم الحالية. من في الغرفة 0 يبقى في الغرفة 0 ، ومن في 1 يذهب إلى 2 ، ومن في 2 يذهب إلى 4 ، إلخ ...

وهكذا أصبحت جميع الغرف ذات الأرقام الفردية فارغة ويمكن للقادمين الجدد أن ينزلوا الفندق.

ما فعلناه هنا مرة أخرى هو أننا أنشأنا تقابلا لأننا أخذنا جميع الموجودين في الفندق وجميع الموجودين في الحافلة وأعطينا لكل واحد منهم رقمًا جديدًا. لذلك أنشأنا تقابلا بين مجموعة الأشخاص و مجموعة الأعداد الطبيعية N (التي تمثل أرقام الغرف)، وبالتالي فإن مجموعة الغرف و مجموعة الأشخاص الحاضرين لهما نفس عدد العناصر وهو اللانهاية ، وهو كاردينال مجموعة الاعداد الطبيعية N.

نفس الشيء يظهر إذا أردنا أن ننشئ تقابلا بين الأعداد الطبيعية الموجبة N ومجموعة الأعداد النسبية (التي تحتوي على أرقام سالبة و موجبة ونسميها Z) حيث أن كاردينال مجموعة الأعداد النسبية هو نفسه كاردينال N حيث يمكننا أن نرقم الأعداد النسبية (ننشئ تقابلا مع N) إذا كنت لا تصدق ذلك فيمكن أن نخصص الأرقام الزوجية في N لأرقام موجبة في Z ويتم تخصيص الأرقام الفردية في N للأرقام السالبة في Z.

كل هذه المجموعات التي لها نفس الكاردينال مثل N (لأنه يمكننا ترقيمها)، نقول إنها قابلة للعد.

2.3. اللانهاية في المجموعات الغير قابلة للعد

لكن السؤال هنا، هل توجد مجموعات لا نهائية أكبر من مجموعة الأعداد الصحيحة الطبيعية، حيث لا نستطيع أن نرقمها؟ بمعنى أنها غير قابلة للعد.
لمحاولة الإجابة على هذا السؤال ، يمكننا العودة إلى فندق هيلبرت. 

لقد رأينا أن فندق هيلبرت ، حتى لو كان ممتلئًا بالنزلاء، وجاءت حافلة مليئة بعدد لا نهائي من الناس، ما زلنا نستطيع أن ندخل الجميع داخل الفندق، لذلك لإنشاء مجموعة لا نهائية أكبر من مجموعة الأعداد الطبيعية ، سيتعين علينا التفكير بطريقة مختلفة.

لنتخيل هذه المرة أن عددا لانهائيا من الحافلات تحتوي كل منها على عدد لانهائي من الناس قد وصلوا للفندق. ماهو الحل هذه المرة. قد يبدو الأمر معقدا ولا يمكن ايجاد حل لإدخال الجميع للفندق.

لكن هناك حل، نأخذ جميع الأشخاص الموجودين في الفندق في البداية وننقلهم إلى الغرف التي أرقامها أعدادًا أولية،  صاحب الغرفة 0 ينتقل الى الغرفة 2 وصاحب الغرفة 1 ينتقل الى الغرفة رقم 3 وصاحب الغرفة 2 ينتقل الى الغرفة 5 ... وهكذا بحيث جميع النازلين في الفندق تكون أرقام غرفهم أعدادا أولية. حيث يوجد عدد لانهائي من الأعداد الأولية ، لذا لا توجد مشكلة في إدخال عدد لا نهائي من الناس في الفندق.

من الواضح أنه في كل مرة نحاول فيها صنع مجموعة يمكن تكون أكبر من مجموعة الأعداد الطبيعية يتضح بعد ذلك أن لهما نفس الكاردينال، ويتبين أنها مجموعات قابلة للعد. 

لمحاولة إنشاء مجموعة أكبر من الأعداد الطبيعية، نحتاج إلى مجموعة لا يمكن عدها، (أي لا يمكن ترقيمها).

هناك مجموعة يعرفها الجميع ولا يمكن ترقيمها، وهي مجموعة الأعداد الحقيقية R. بشكل بديهي ، نشعر أن الأعداد الحقيقية أكثر من الأعداد الصحيحة لأن الأعداد الحقيقية تشكل سلسلة متواصلة ، في حين أن الأعداد الصحيحة هي شيء غير متواصل (بمعنى أن هناك فراغ بين كل رقمين متتاليين في الاعداد الطبيعية).

هل من الممكن أن نثبت بطريقة رياضية أن الأعداد الحقيقية أكبر من الأعداد الصحيحة؟ الإجابة هي : نعم نستطيع.

لن أقدم لكم هنا الشرح بالتفصيل ، لكنه ليس معقدًا للغاية. وقد قدمه عالم رياضيات مشهور اشتغل كثيرًا على مسألة اللانهايات يسمى جورج كانتور.

استعمل جورج كانتور طريقة مشهورة في الرياضيات تسمى مبدأ التناقض (reductio ad absurdum) حيث افترض أنه يمكننا ترقيم مجموعة الأعداد الحقيقية ووضح أنه في هذه الحالة ، ننجح دائمًا في إنشاء عدد حقيقي لم يكن في ترقيمنا في البداية ، لذلك لدينا تناقض وهذا يوضح أن مجموعة الأعداد الحقيقية غير قابلة للعد.

واستنتج كانتور أن كاردينال مجموعة الأعداد الحقيقية هو أيضًا اللانهاية، لكنها لانهاية اكبر من اللانهاية التي تمثل كاردينال الاعداد الطبيعية، ويمكن أن تسمي هذه اللانهاية بأوميغا (Ω) مثلا.

عند التعامل مع اللانهايات في الأعداد الحقيقية، نلاحظ أشياء غريبة أيضا كما حدث عندما تحدثنا عن النهايات في الاعداد الطبيعية.

فمثلا عندما نتخيل جميع الأعداد الحقيقية التي تتراوح  بين 0 و 1، نعتقد أن عددها أقل من عدد جميع الاعداد الحقيقية الاخرى (لأنها جزء من الأعداد الحقيقية)، لكن الأمر ليس كذلك، فهما متساويان إلى حد ما !

 لتوضيح ذلك ، يكفي إيجاد تقابل بين هذه المجموعة ومجموعة الأعداد الحقيقية.

فمثلا هذه الدالة (f(x) = tan(π (x-1/2) تربط جميع الأرقام الحقيقية التي تقع بين 0 و 1 بكل الأرقام الموجودة في الأعداد الحقيقية (التي تقع بين اللانهاية السالبة واللانهاية الموجبة) وبالتالي فإن هذه المجموعة ومجموعة الأعداد الحقيقية لها نفس الكاردينال أوميغا (Ω).

هناك الكثير من الفارقات من هذا النوع لكن لا يسعنا أن نذكرها جميعا. بل ويمكننا أن نذهب إلى أبعد من ذلك ونصنع مجموعة يكون كاردينالها أكبر من Ω.

3.  فرضية الاستمرارية و مبرهنات عدم الاكتمال لغودل

ولكن هناك سؤال آخر مثير للاهتمام ، وهو ما إذا كانت هناك مجموعات لا نهائية أكبر بطريقة ما من الأعداد الصحيحة الطبيعية ولكنها أصغر من الأعداد الحقيقية.

اعتقد كانتور أن مجموعات من هذا النوع ليست موجودة في الواقع لكن لم يجد طريقة للبرهان عليها وأطلق على هذه الفكرة اسم فرضية الاستمرارية أو فرضية الاتصالية (بالانجليزية continuum hypothesis).

هناك عدد معين من علماء الرياضيات خلال القرن العشرين الذين حاولوا إثبات  فرضية الاستمرارية أو العثور على مثال مضاد لها، أي تصنيع مجموعة أكبر من الأعداد الصحيحة ، ولكنها أصغر من الأعداد الحقيقية.

يمكن للمرء أن يفكر لأول وهلة في مجموعة الأعداد الكسرية، لكن العدد الكسري متكون من بسط و مقام أي من زوج من الاعداد الطبيعية ويمكن تسميتها بمجموعة N²، ويمكن اثبات أن كل مجموعة اعداد تتكون من ازواج من الاعداد الطبيعية هي ايضا قابلة للعد أي لها نفس كاردينال مجموعة الأعداد الطبيعية N لذا فإن مجموعة الكسور ليست أكبر من مجموعة الأعداد الطبيعية .

لمدة طويلة من الزمن كان علماء الرياضيات يكافحون للتوصل الى حل لفرضية الاستمرارية، لكن في منتصف القرن العشرين ، تم إثبات أن هذا السؤال غير قابل للحسم. 

ربما تكون قد سمعت بالفعل عن هذه الفكرة وعن نظرية جودل التي تنص على أنه في الرياضيات ، عند مستوى معين من التعقيد ، هناك افتراضات لا يمكن إثباتها أو إبطالها. وهذه النظرية هي من الأفكار التي غيرت نظرتنا للعلم في القرن العشرين إضافة الى نظرية الفوضى و ميكانيكا الكم.

إن فرضية الاستمرارية من المسائل التي لا يمكن البت فيها، أو بالأحرى تعتمد إجابتها على نظام البديهيات الذي يستخدمه المرء.

إذا كان هذا كله معقدا جدا بالنسبة لك ، فكن مطمئنًا أنني سأتوقف عند هذا الحد ، لكنني أعدك ، يومًا ما سأكتب مقالا حول نظرية جودل بالتفصيل.