فرضية ريمان | مسألة بمليون دولار

فرضية ريمان | مسألة بمليون دولار

إن علم الرياضيات يعتبر من العلوم الأساسية في فهم الكون، ولكن توجد فيه بعض المسائل الرياضية المعقدة لدرجة حيرت العلماء لعقود. في هذه المقالة سنتطرق إلى إحدى المسائل المعقدة والتي من الصعب إيجاد اجابة بسيطة لها ألا وهي فرضية ريمان.

1. ماهي فرضية ريمان

تعتبر فرضية ريمان إحدى مسائل الألفية، مثل مسألة P و NP (التي عرضناها في مقال سابق) وهي 7 مسائل معقدة جدا لدرجة أن معهد كلاي الفرنسي خصص مبلغ مليون دولار لأي أحد يتمكن من حل إحدى هذه المسائل. ففرضية ريمان هي فرضية طرحها عالم الرياضيات الألماني برنارد ريمان سنة 1859 وإلى حد يومنا هذا لم يتمكن أحد من إثباتها أو نفيها، بالرغم من أن أغلب علماء الرياضيات والباحثين يعتبرون أنها صحيحة على الأغلب.

وبشكل عام، توجد في الرياضيات بعض الأوضاع المشابهة، بمعنى أنها توجد بعض المسائل التي يعتبرها علماء الرياضيات صحيحة رغم عدم وجود برهان واضح على صحتها. لكن لماذا إذًا تعتبر فرضية ريمان مسألة إستثنائية وتختلف عن باقي المسائل؟

فرضية ريمان هي فرضية تقترح وجود رابط بين قسمين مختلفين تماما من أقسام الرياضيات وهما الأعداد الأولية و التحليل العقدي، واللذان يعتبران بعيدان كل البعد عن بعضهما. ولفهم هذا الرابط الذي تضعة فرضية ريمان سنتكلم أولا عن الأعداد الأولية ثم عن التحليل العقدي وسيتضح بعد ذلك الرابط الذي تقترحه فرضية ريمان.

2. الأعداد الأولية

2.1 ماهي الأعداد الأولية

الأعداد الأولية هي أعداد لايمكن قسمتها على أي عدد آخر بخلاف نفسها والرقم 1. مثل 2 و 3 و 5 و 7 و 11 و 13... ومنذ فجر التاريخ، يطرح علماء الرياضيات الكثير من الأسئلة حول هذه الأعداد الأولية مثل: كم يبلغ عددها؟ كيف تتوزع بين الأعداد؟ كيف يمكن إيجادها؟...

بعض هذه الأسئلة تم الاجابة عليها منذ زمن طويل، فعلى سبيل المثال أثبت العالم إقليدس قبل 2000 سنة أن الأعداد الأولية غير متناهية، ونعلم أيضا أن هذه الأعداد الأولية تصبح نادرة شيئا فشيئا كلما كبرت. فمثلا بين 0 و 100 يوجد 25 عددا أوليا، وبين 1000 و 1100 يوجد 16 فقط، وبين 1000000 و 1000100 يوجد فقط 6.

2.2 دالة التوزيع

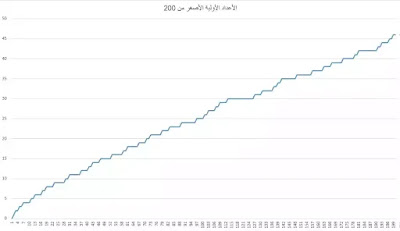
لفهم طريقة توزع هذه الأعداد الأولية ولتمثيلها، سنستعمل دالة بسيطة تسمى دالة التوزيع، وهي دالة تعطيك كمية الأعداد الأولية التي هي أصغر من عدد معين x. تتميز هذه الدالة بشكلها الذي يشبه الدرج، فهي تزيد ب 1 كلما صادفنا عددا أوليا.

لسوء الحظ، لا توجد صيغة معينة لهذه الدالة، فكي نمثلها لابد لنا من البحث عن كل الأعداد الأولية الأصغر من العدد x. ثم بعد ذلك، عن طريق قائمة هذه الأعداد يمكن رسم الدالة. وهذه العملية مجهدة كثيرا ومتعبة، خصوصا إذا كان العدد x كبيرا، وهذا لأننا مجبرون بطريقة أو بأخرى بالمرور عبر كل الأعداد بين 0 و x لكي نزيل الأعداد التي ليست أولية.

فلا نستطيع إذًا رسم دالة التوزيع دون أن تكون لدينا قائمة الأعداد الأولية التي سنمثلها. لكن توجد بعض الدوال القريبة من دالة التوزيع والتي نملك مسبقا صيغة رياضية لها.
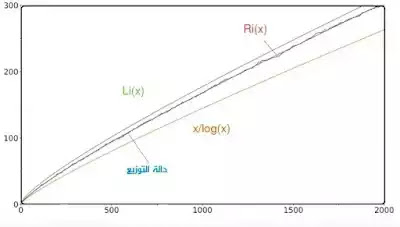
أول هذه الدوال هي الدالة x/log(x) : وهي دالة بسيطة قليلا حيث شكها العام قريب من دالة توزيع الأعداد الأولية. والتي يمكن أن تمكننا من معرفة عدد الأعداد الأولية في ولو بصفة تقريبية، بالرغم من أنها، كما تشاهدون، أصغر قليلا من دالة التوزيع.

لكن توجد مقاربة أخرى أكثر دقة من x/log(x)، ألا وهي دالة اللوغاريتم التكاملي (Integral logarithmic function) وتسمى Li(x) وصيغتها هي :

نلاحظ هنا أن هذه الدالة قريبة جدا من دالة توزيع الأعداد الأولية، أقرب من الدالة السابقة.
أول ما فعله ريمان بخصوص هذه المقاربات القريبة من دالة توزيع الأعداد الأولية هو أنه اقترح صيغة رياضية مشتقة من الدالة Li (x) قريبة جدا من دالة التوزيع، أقرب حتى من الدالة Li (x) ألا وهي الدالة Ri (x) :

إذا قمنا بتمثيل هذه الدالة فسنلاحظ فعلا أنها قريبة جدا من دالة توزيع الأعداد الأولية. مشكلة هذه الدالة، رغم كونها تتبع مسار دالة التوزيع بشكل مثالي، هي كون طبيعتها لا تشبه دالة التوزيع، بمعنى أنها ليست على شكل درج. وبذلك هي لا تخبرنا بالضبط عن مكان وجود الأعداد الأولية بدقة. 

ماذا لو كان لدينا صيغة رياضية تمكّننا من معرفة مكان القفزات الصغيرة في الدالة Ri (x) بحيث تصبح مطابقة تماما لدالة التوزيع وبذلك سنتمكن من معرفة مكان أي عدد أولي؟ هذا ما نجح ريمان بعد ذلك في فعله.

لفهم كيف فعل ذلك، سيتعين علينا الإنتقال إلى فرع من فروع الرياضيات، الذي يبدو من الوهلة الأولى، لا علاقة له بالأعداد الأولية، ألا وهي المجاميع أو السلاسل اللانهائية.

 2.3 السلاسل اللانهائية

في الرياضيات، يمكننا جمع عددين أو ثلاثة أو أكثر، لكن في بعض الأحيان، وفي ظروف خاصة يمكننا جمع عدد لانهائي من الأعداد ونتحصل على عدد معين. فعلى سبيل المثال إذا قمنا بجمع 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 ... إلى ما لانهاية فيمكننا ملاحظة أنها تقترب شيئا فشيئا من الرقم 1 كلما أضفنا أعدادا أخرى. هذه المجاميع يسميها علماء الرياضيات سلاسل أو متسلسلات، ويوجد الكثير من الأمثلة في الرياضيات. لكن ما علاقة هذه السلاسل بالأعداد الأولية و مقاربة ريمان؟

في بداية القرن الثامن عشر، وقبل ريمان، قدم العبقري السويسري ليونارد أويلر الإجابة عن هذا السؤال، فقد أخذ المتسلسلة التالية ( S(x) بحيث x يجب أن يكون أكبر من 1) و أعاد صياغتها بحيث تظهر داخلها الأعداد الأولية كلها :

فكما نلاحظ في الصيغة الثانية، أن أويلر حوّل السلسلة إلى جذاء لانهائي يحمل في طياته الأعداد الأولية.
إن صيغة أويلر يمكن ان تظهر للبعض على أنها غريبة نوعا ما، لكنها أثبتت أنه يوجد رابط عميق بين المتسلسلات والأعداد الأولية. وما فعله ريمان بعد ذلك هو إظهار هذا الترابط بشكل أكثر وضوحا.

3. الأعداد العقدية و دالة ريمان "زيتا"

كما قلنا في السابق، إن الدالة S(x) لا يمكن أن تكون صالحة إلا إذا كان العدد x أكبر من 1. ما فعله ريمان، هو إثبات أنه يمكن تغيير هذه الدالة بحيث يصبح x ينتمي إلى مجال أوسع، ألا وهو مجال الأعداد العقدية.

3.1 ماهي الأعداد العقدية

العدد العقدي هو عدد مركّب على شكل z = a +b*i بحيث a و b عددان حقيقيان، أما  i فهو عدد تخيلي بحيث إذا ضربناه في نفسه نتحصل على العدد -1.
الطريقة الأكثر بساطة لتمثيل الأعداد العقدية هو اعتبار أن كل عدد عقدي هو نقطة في مستو ثنائي الأبعاد وإحداثياته هيa و b ونسمي الجميع بالمستوي العقدي (Complex plan). والأعداد الحقيقية هنا ترسم جميعها على المحور x الأفقي أما الأعداد التخيلية فعلى المحور y العمودي.

3.2. دالة ريمان "زيتا" - دالة ريمان المعدلة

كما قلنا سابقا، أن ما فعله ريمان، هو تمديد مجال دالة أويلر من جزء معين من المحور x لتصبح صالحة على كامل المستوي العقدي. هذه الدالة الجديدة تسمى بالدالة زيتا.

تعرفنا الآن على دالة ريمان الشهيرة زيتا، والتي تم اكتشافها عن طريق تمديد مجال دالة أويلر. واستطعنا أن نفهم أن لها علاقة وطيدة بالأعداد الأولية. لنعد الآن الى موضوعنا الأساسي، الأعداد الأولية.
في السابق، في قسم الأعداد الأولية، قلنا أن الدالة Ri(x) قريبة جدا من من دالة توزيع الأعداد الأولية لكنها لا تشبهها وذلك لأن دالة التوزيع تتخذ شكلا مدرجا.

ما اكتشفه ريمان، هي دالة مشتقة من الدالة Ri(x) وتتخذ شكلا مدرجا، بحيث تكون مماثلة تماما لدالة التوزيع. حيث أخذ الدالة Ri(x) وطبق عليها بعض التعديلات الصغيرة. فأخذ الدالة Ri(x) وطرح منها Ri(x^z) حيث z هي النقاط الموجودة في المستوي العقدي و التي تصبح عندها الدالة زيتا مساوية لصفر. 

أصبحت دالة ريمان المعدلة هكذا:

حيث z1 و z2 و z3 و z4 و z5 ... هي كل الأعداد العقدية التي تصبح عندها الدالة زيتا مساوية لصفر.(وتسمى أصفار الدالة زيتا).

وهذا يعني أننا إذا عرفنا كل هذه الأعداد العقدية التي تصبح عندها الدالة زيتا مساوية لصفر فعندها سنجد الصيغة الرياضية لدالة توزيع الأعداد الأولية ونستطيع عندها معرفة أي عدد أولي مهما كان، دون استعمال الطريقة الكلاسيكية.
الآن يجب علينا فقط إيجاد هذه النقاط.

4. الدالة زيتا، ونص فرضية ريمان

4.1. الأصفار غير البديهية في الدالة زيتا

قلنا قبل قليل أن معرفة صيغة الدالة التي ستمكننا من معرفة أي عدد أولي، مرتبطة ببعض الأعداد العقدية التي تصبح عندها الدالة زيتا منعدمة (مساوية لصفر). إذا قمنا بتمثيل الدالة زيتا في المستوي العقدي فسنلاحظ عدة نقاط حيث تنعدم الدالة زيتا.

أول مجموعة من النقاط هي النقاط الموجودة على المحور x وتكون سلبية وزوجية. تسمى هذه النقاط الأصفار البديهية.

أما النقاط الأخري فتبدو مصطفة على المستقيم العمودي الذي يقطع المحور x في النقطة 1/2. أي أنها مجموعة من الأعداد العقدية ذات الجزء الحقيقي = 1/2. تسمى هذه النقاط بالأصفار غير البديهية.

4.2. نص فرضية ريمان

لكن هل كل الأصفار غير البديهية في الدالة زيتا جزؤها الحقيقي مساو ل 1/2؟ هل كل الأصفار غير البديهية توجد على المستقيم الذي يقطع المحور x في النقطة 1/2؟

تقول فرضية ريمان أن ذلك صحيح، بمعنى أن كل الأصفار غير البديهية في الدالة زيتا جزؤها الحقيقي مساو ل 1/2. 

وكما قلنا سابقا، أن معرفة هذه الأصفار مهمة جدا فهي الطريقة الوحيدة التي عن طريقها يمكننا من معرفة دالة توزيع الأعداد الأولية. يعتقد أغلب علماء الرياضيات أن فرضية ريمان صحيحة إلى حد كبير، فإلى حدود هذه اللحظة، تمكنّا من إيجاد حوالى عشرة آلاف بليون صفر على هذا المستقيم، ولا يوجد أي صفر غير بديهي خارجه. لكن رغم ذلك، هذا العدد الكبير لا يضمن أنه لا توجد نقطة خارج هذا المستقيم فلا بد من دليل رياضي على ذلك.

إذا تمكنت من أثبات هذه الفرضية، بطريقة رياضية، أو إيجاد نقطة واحدة خارج المستقيم 1/2 وبذلك إثبات خطإ هذه الفرضية، فستحصل على المليون دولار.

لكن هذه بالطبع ليست بالمهمة السهلة، فكما قال عالم الرياضيات دافيد هيلبرت قبل قرن من الآن أنه إذا نام ثم استفاق بعد 1000 سنة، فأول ما سيسأل عنه هو هل تم إثبات فرضية ريمان أم لا.