تأثير الفراشة ونظرية الفوضى
تأثير الفراشة ونظرية الفوضى
عندما يسمع أحدنا كلمة "فوضى" يخيل إليه أنها تعني عدم الانتظام المطلق، لكن في علم الرياضيات، كل فوضى تخفي وراءها نوعا من الانتظام.
ربما قد سمعت من قبل عن تأثير الفراشة. سنحاول في هذا المقال أن نفهم أسس هذه النظرية و كيف غيرت نظرتنا للعالم من حولنا.
الأنظمة الديناميكية
تنتمي نظرية "الفوضى" إلى فرع من فروع الرياضيات يسمّى "دراسة الأنظمة الديناميكية". والنظام الديناميكي هو كل شيء يتغير مع مرور الوقت.
يوجد في الفيزياء الكثير من الأمثلة مثل حركة الكواكب حول الشمس، ومسار طلقة مدفع، وحركة بندول الساعة... وفي الكيمياء أيضا هناك التفاعلات الكيميائية، والكثير من الأمثلة أيضا في البيولوجيا وعلم الإقتصاد و الإلكترونيك وغيرهم...
الأنظمة الديناميكية البسيطة
عند دراسة الأنظمة الديناميكية، كثيرا ما يبدأ علماء الرياضيات بدراسة نظام "مثالي" وبسيط، ودائما مايكون هذا النظام موصوفا بمعادلة تصف تطوره مع مرور الوقت. لنأخذ حركة البندول كمثال :
المعادلة التي كتبت على الصورة تصف حركة البندول مع الوقت.
بشكل عام، تعد الأنظمة البسيطة، مثل هذا البندول البسيط، أنظمة حتمية أي أنه من السهل توقع حركتها في أي وقت تشاء ولا يوجد مجال لتدخل الصدفة في حركتها، ولن يكون الفارق كبيرا بين النتائج إذا غيرنا قليلا في الظروف الأولية لهذا النظام، ففي حالة هذا البندول مثلا لن يكون الفارق كبيرا بين النتائج إذا كانت قيمة الزاوية الأولية 70 أو 72 درجة، ستحصل نفس النتائج تقريبا والبندول سيتحرك تقريبا بنفس الوتيرة.
الأنظمة الديناميكية المركّبة
منذ عصر نيوتن، كانت هناك فكرة أن نفس الأسباب تؤدي الى نفس النتائج وهذه هي الحتمية. وكذلك الأسباب القريبة من بعضها تؤدي إلى نتائج متقاربة.
وهذه تعتبر-نوعا ما- إحدى أسس التجارب العلمية، ففي التجارب لن نستطيع قياس كل شيء بدقة مثالية.
لكن هذه المقاربة لاتعمل دائما بشكل صحيح في جميع الأنظمة، لنأخذ لعبة البلياردو كمثال، إذا غيرت ولو جزءا صغيرا جدا في الزاوية الأولية أو في مقدار قوة الضربة فستحصل على نتائج مختلفة تماما عما كنت تتوقعه.
إذا كان هناك نظاما يمثل هذه الفكرة بشكل جيد فهو البندول المزدوج (بندول معلّق في طرف بندول آخر) :
نلاحظ هنا أن المعادلات التي تصف حركة البندول المزدوج أعقد بكثير من البندول البسيط. دون أن نتعمق في تفاصيل المعادلة بشكل كبير، فإن حركة البندول المزدوج فوضوية ولا يمكن التنبؤ بها مثل البندول البسيط.
إذا وضعنا بندولين مزدوجين بجانب بعضهما ولكن يختلفان فقط بمقدار 0.1 درجة، سنلاحظ أنه بعد وقت معين سيكون الاختلاف بين حركة البندولين كبير جدا. وهذا يعود الى كون حركة الأنظمة المركبة مثل البندول المزدوج تعتمد بشكل كبير على الظروف الأولية، فالتغير في هذه الظروف ولو بشكل بسيط جدا ينتج عنه فارق كبير في النتائج.
هذه الظاهرة (كون تغيّر بسيط في البداية يُنتج فارقا كبيرا في النتائج) تسمى بتأثير الفراشة.
تاريخ نظرية الفوضى
إن قصة تأثيرالفراشة أتت في البداية من علم الطقس والأرصاد الجوية، فالمناخ يعتبر أيضا نظاما ديناميكيا يتغير مع مرور الوقت كالبندول المزدوج، لكنه أعقد بكثير، فكما تعلم، إن توقع حالة الطقس بعد عدة أيام يعد معقدا بشكل كبير، وهذا يعود الى وجود عدة عوامل يجب أخذها بالاعتبار كسرعة الرياح وضغط الهواء ودرجة الحرارة... وفي أي نقطة من الغلاف الجوي على الأرض !!
لفهم تطور حالة الطقس، قام عالم الطقس الامريكي ادوارد لورينز بعمل نموذج بسيط لتطورالطقس في الغلاف الجوي يعتمد فقط على ثلاثة عوامل. بدأ لورينز بثلاث معادلات تصف حركة الهواء في الجو:
بعد ذلك أخذ قياسات الجو ثم بدأ في محاكاة تغيّر هذه العوامل الثلاثة مع مرور الوقت. لكن في يوم ما، لورينز أوقف هذه المحاكاة. ثم أراد بعد ذلك أن يكملها، هناك طريقتان لذلك، إما أن يبدأ من البداية ويعيد ما فعله المرة السابقة ثم يكمل بعده وهنا سيخسر الكثير من الوقت، أو يبدأ من النقطة التي توقف عندها، بمعنى أن يدخل البيانات التي تحصل عليها من خلال المحاكاة السابقة كنقاط بداية ثم يبدأ المحاكاة، وهنا بالطبع اختار الخيار الثاني.
هنا لاحظ لورينز أن تطور البيانات بدأ تقريبا مماثلا للمرة السابقة، ثم عند نقطة معينة يبدأ الاختلاف يظهر ثم يتفاقم إلى أن تحصل على بيانات مختلفة تماما عن المرة السابقة.
هنا بالطبع لورينز كان يظن أنه أخطأ في إدخال البيانات أو أن الحاسوب الذي يستعمله به خطب ما. ثم بعد ذلك وجد السبب الحقيقي : عوض أن يدخل البيانات كاملة (أعداد بها أربعة أرقام بعد الفاصلة) أدخل بيانات برقمين فقط بعد الفاصلة. لم يكن أحد من المجتمع العلمي يعتقد أن هذا الفارق البسيط يمكن أن يحدث فرقا بهذه الضخامة.
عندما قدم اكتشافه في مؤتمر علمي بعد عدة سنوات، كان عنوان محاضرته:
" Does the Flap of a Butterfly's Wings in Brazil set off a Tornado in Texas" بمعنى "هل أن رفرفة أجنحة فراشة في البرازيل يمكن أن تحدث إعصارا في تكساس". ومن هنا نشأ اسم تأثير الفراشة.
إن مصطلح تأثير الفراشة قد أصبح شائعا الى حد كبير بين الناس لكن أغلبهم لا يفهمون جوهره بشكل كامل، ما قصده لورينز بهذه العبارة هو أنه إذا أردت توقع نشأة إعصار في وقت محدد في تكساس فلا بد لك أن تضع في اعتبارك كل التغيرات الطفيفة في حركة الهواء حتى حركة أجنحة فراشة، لأن ذلك الفارق البسيط في حركة الهواء الذي أحدثته أجنحة الفراشة، سيحدث تغييرات أكبر بعد مرور وقت معين، وهذه التغيرات، إذا أضيفت لها تغيرات صغيرة أخرى من عوامل أخرى فقد تنشئ تغييرات أكبر وهكذا...
الفوضى المنتظمة - مفهوم الجاذب
إن نظرية الفوضى مرتبطة كثيرا ببعض المفاهيم الرياضية و بنوع معين من الدوال الذي يمتلك خصائص فريدة، والذي يبدو في الظاهر يتصرف بشكل عشوائي لكنه يخفي وراءه نوعا من الانتظام.
الدوال اللوجيستية
لنأخذ عددا معينا (لنسميه x) أصغر من 1 و أكبر من 0، ونطبق عليه هذه الدالة 4x(1-x).
فإذا كان مثلا x =0.37 فسنتحصل على 0.93
حسنا فلنأخذ الآن هذا العدد 0.93 و نطبق عليه نفس الدالة سنحصل على 0.25 ونعيد نفس الشيء مع هذا العدد 0.25 وهكذا..، كل عدد نحصل عليه نضربه في 4 ثم نضرب الجميع في الفارق بينه وبين 1.
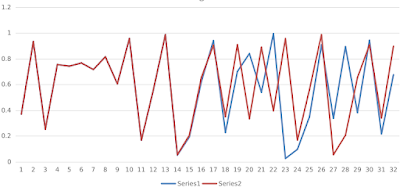
ثم نرسم مخطط تغيير هذه الدالة. سنجد الشكل التالي (اللون الأزرق في الشكل التالي).
الآن إذا غيرنا العدد الذي استعملناه أول مرة و نضيف إليه 0.000001 (جزء من المائة ألف) بحيث يصبح 0.370001 ونعيد نفس خطوات المرة السابقة مع نفس الدالة ثم نرسم المخطط (اللون الأحمر).
- هذه الدالة تتغير بشكل غير منتظم وعشوائي، أي أنه لايوجد نمط معين تتبعه
- رغم الفارق البسيط جدا في الظروف الأولية فإن الفرق في النتائج سيظهر بعد خطوات كافية ثم يتسع. وهذا مثال جيد عن الأنظمة الفوضوية.
الجاذب
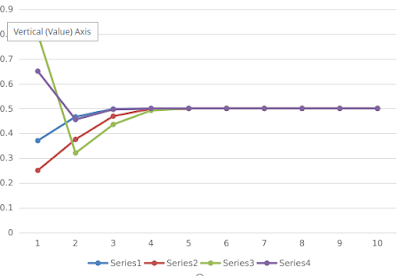
ما يجعل هذه الدالة مثيرة جدا للإهتمام هو أنه إذا غيرنا قليلا فيها فإن تصرفها سيختلف تماما. فلنجرب ذلك: إذا غيرنا الرقم 4 وبدلناه ب 2 لتصبح الدالة 2x(1-x). وقمنا باختيار أربعة نقاط بداية وفعلنا نفس ما فعلناه في السابق فسنحصل على الشكل التالي:
نلاحظ هنا أنه مهما اختلف الرقم الذي أدخلناه في البداية فإن الدالة تتجه دائما نحو الرقم 0.5 بمعنى أنه بعد خطوات كافية فسيصبح الرقم الذي تحصلت عليه دائما 0.5 وهذا العدد اسمه الجاذب.
إذا غيرنا الدالة 2x(1-x) مجددا وبدلنا 2 ب 1.6 فسيصبح الجاذب تقريبا 0.38، وإذا غيرنا 2 ب 2.8 فسيصبح الجاذب 0.64، يمكنك تجربة ذلك بواسطة برنامج Excel إذا أردت.
إذا غيرنا الآن 2 في الدالة ب 3.1 فسيصبح لدينا جاذبين اثنين وهما 0.76 و 0.56.
وإذا غيرنا 2 في الدالة ب 3.5 فسيصبح لدينا أربعة من الجاذب. و إذا عوضنا 2 ب 3.56 فسيصبح لدينا 8.
إذا كان الرقم أقل من 3 فالدالة تملك جاذبا واحد، ثم بعد ذلك يصبح لدينا 2 ثم 4 ثم 8.
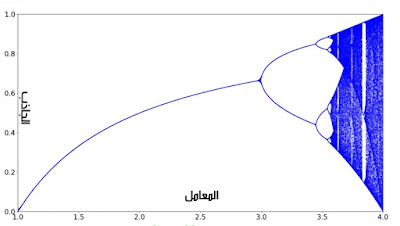
عند 3.57 يصبح سلوك الدالة فوضويا ولا تمتلك أي جاذب مثل الدالة 4x(1-x) التي تحدثنا عنها في البداية.
لكن عند النظر عن قرب، نلاحظ وجود أماكن بيضاء حيث يختفي السلوك الفوضوي للدالة ويصبح عندها جاذب أو أكثر، وإذا قربنا أكثر سنجد أماكن فوضوية أصغر موجودة داخل تلك المنطقة البيضاء. وهذه الأماكن الفوضوية ايضا تحتوي على مناطق بيضاء حيث عدد الجاذب محدود وهكذا الى ما لانهاية، كلما تقرب أكثر ستجد أماكن فوضوية وداخلها أماكن بيضاء...
جاذب لورينز
إن مفهومي الفوضى و الهندسة الكسيرية كثيرا ما يكونان مرتبطان ببعضهما بشكل أو بآخر. ففي النظم الفوضوية، نصادف في بعض الأحيان حالات كسيرية كما رأينا في المثال السابق.
رأينا أن الدالة اللوجيستية تتسم أحيانا بسلوك عشوائي، لكن هل الحال كذلك بالنسبة لنظام لورينز؟ بمعنى هل أن متغيرات لورينز x وy و z الذين تم وصفهم في معادلات لورينز السابقة يتغيرون بطريقة عشوائية أم أن هناك حالة من الإنتظام تتجه إليها حالة الطقس دائما.
لمعرفة ذلك لابد من رسم مخطط يصف تغير هذه المتغيرات حيث نضع نقطة في الفضاء والتي تمثل حالة الطقس في وقت معين، ثم نلاحظ تحركها مع مرور الوقت. وهذا ما سنشاهده إذا طبقنا المعادلات.
ما يبينه هذا الرسم هو أن تطور حالة الطقس "يدور" حول نقطة معينة، ثم من وقت لآخر تنتقل لتدور حول نقطة أخرى ثم تعود، أي أن حالة الطقس تتردد حول نقطتين اثنتين وتصنع نمطا ذا مظهر شبيه بأجنحة فراشة ولا تتحرك بشكل عشوائي كما كنا نظن. هتين النقطتين يسميان ب جاذب لورينز.
لكن هذين الجاذبين ليسا كالجاذبين اللذين يميزان الدالة اللوجيستية، بمعنى أن حالة الطقس لا تنتقل بينهما بشكل دوري ولكن بشكل عشوائي.
يمكن تفسير هذين الجاذبين بشكل مبسط على أن الأول يمثل حالة الطقس الجيدة والآخر يمثل حالة الطقس السيئة. ويوجد في العالم أيضا الكثير من الأمثلة عن الظواهر التي تتسم بسلوك قريب من حالة الطقس هذه، مثل الحقل المغناطيسي للأرض.
ما لايعلمه الكثيرون هو أن هذا النمط الذي رسمته حالة الطقس يتميز أيضا ببنية كسيرية. أي أنه اذا قمنا بتكبير جزء من هذه "الفراشة" التي رسمتها حالة الطقس، فسنجد أن هذا الجزء يتكون في الحقيقة من عدة طبقات من هذه "الخيوط" التي ترسمها النقطة المتحركة وكل طبقة تتكون هي أيضا من طبقات أصغر.
بمعنى أن تلك "الأجنحة" ليست رسما ثنائي الأبعاد ولكنه ثلاثي الأبعاد ويتكون من عدة طبقات.
إن مفهوم جاذب لورينز هو مفهوم في غاية الأهمية حيث بين لنا أن أي نظام فوضوي لا يتسم بالضرورة بسلوك عشوائي مطلق، صحيح أن تطوره يبدو في الظاهر غير قابل للتوقع لكن إذا راقبت سلوكه بشكل كاف فستجد أنه يتبع نمطا معينا، ويتجه حول جاذب.
توجد الكثير من الأمثلة حول التصرف العشوائي للظواهر الطبيعية، مثل علم الفلك حيث أن السلوك العشوائي وغير المنتظم يظهر في نظام مكون من ثلاثة أجرام أو أكثر. كذلك في لعبة البالياردو و ميكانيكا الموائع وغيرها.
إن فكرة وجود أنظمة فوضوية ولا يمكن التنبؤ بها أثارت ازعاج المجتمع العلمي في بداية ظهورها، حيث أن بعض الأحداث رغم كونها حتمية الحدوث، توجد أمامنا عقبة أساسية وهي كوننا لا نستطيع التنبؤ بها بدقة مهما كانت قوة حواسيبنا أو معداتنا التي نستعملها.
مثلت نظرية الفوضى، إضافة الى ميكانيكا الكم و نظرية جودل، ثلاثة اكتشافات عظيمة ميزت القرن العشرين، وأظهرت لنا عجز البشر عن معرفة كل شيء بدقة في هذا العالم من خلال العلم.
شاهد أيضا : مسألة المليون دولار P=NP




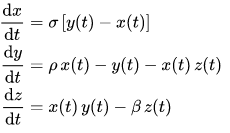


تعليقات
إرسال تعليق
اكتب تعليقك اذا كان لديك اي تساؤل او اضافة